HWK 6-1.

a. W_net = W₁ + W₂ = eE₁ l₁ + eE₂ l₂ and i₁ = nA₁uE₁ = i₂ = nA₂uE₂ , from whence, E₂ = (A₁ /A₂) E₁. Place this in the equation above and solve for E₁, etc.

b. v₁ = uE₁ = l₁/ Dt₁ , Dt₁ = l₁ / uE₁, similarly, Dt₂ = l₂ / uE₂ so total time Dt = l₁ / uE₁ + l₂ / uE₂

c. Dt_ss = (.65 m) / (speed of lite)

d. i = n A₁ u E₁

HWK 6-2. a. 3x10¹⁷ (same as A)

b. i = nAuE = nAuF _NC s / (el_new), l_new = (2/3)l_old , so i_new = (3/2) l _old, assuming u doesn't change.

c. No, because u does not change.

d. , since E = i / (nA₁u), A₃ = 2A₁ , which implies that E₃ = E₁ / 2

W = F_NC s = 3 e L E₁ = 3 e L (i₁ / (nA₁u)

= e L(2E₁ + E₁/2) = (5/2) e l (i_new / (nA₁u) dividing, we get

(i_new / i_old) = 5/6

HWK 6-3. a. u₂ = 3 u₁, find i₂ in terms of i₁ : i₂ = i₁. Find E₂ in terms of i₁ and E₁

i₂ = nAu₂ E₂ = nA3u₁ E₂ = nAu₁ E₁, from whence, E₂ = E₁ / 3

b. F_NC s = e.[E₁ + E₂ ]= e l (4/3) E₁ = e l (4/3)(i₁ / (nAu₁)) = el E_o = el (i_o /(nAu₁)) from whence, i_o = (4/3) i₁.

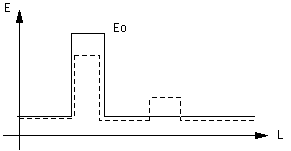
c. i = nAuE. If i is constant throughout the circuit, wherever A is large, E must be small. (Assuming n and u do not change.)

d. E_o = E₁ + E₂ = E₁ + E₁ /3

HWK 6-4. Conservation of Energy implies that W_net = F_NC s = e L₁ + eL₂ E₂ , and i = nA₁ uE₁ = nA₂ u E₂, from whence, E₁ = i/(nA₁ u) , E₂ = i/(nA₂ u), which, when substituted into the above equation , yields,

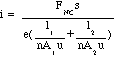
HWK 6-5. you figure it out.