Welcome to

Reality Calculus 2

 

 

OVERVIEW OF RC 2

 

Diff. & Int. of  exp and log functions

Integration Formulas (Heavy Duty Drill)

Integration Applications -

     Geometric:

           Volumes, arclength & Surface areas

     Centers of Mass

     Moments of Inertia

     Work and Electricity

L' Hopital's Rule

Conic Sections

Parametric Equations

Polar, Spherical & Cylindrical Coordinates

Infinite Series
Calculus  DIFFERENTIATION AND INTEGRATION Table ( u = u(x))

 

1.  Dx(c) =

2.  Dx(c f(x)) =

3.  Dx(xn) =

4.  Dx(un) =

5.  Dx(f ± g) =

6.  Dx(fg) =

7.  Dx(f/g)=

8.  Dx(f(u(x)) =

9.  Dx(sin u) =

10.  Dx(cos u) =

11.  Dx(tan u) =

12.  Dx(csc u) =

13.  Dx(sec u) =

14.  Dx(cot u) =

15.  Dx(eu) =

16.  Dx(au) =

17.  Dx(ln u) =

18.  Dx(logau) =

19.  Dx(Arcsin u) =

20.  Dx(Arctan u) =

21.  Dx(Arcsec u) =

22.  Dx(sinh u) =

23.  Dx(cosh u) =

24.  Dx(tanh u) =

25.  Dx(sech u) =

26.  Dx(csch u) =

27.  Dx(coth u)

1.  º c dx =

2.  º c f(x)dx = cºf(x)dx

3.  _xndx =                              for n ­ -1

4.  _unu'dx = º un du =                       for n ­ -1

5.  º(f ± g)dx =

6.  _sin u du =

7.  _cos u  du =

8.  _sec2 u  du =

9.  _csc2u  du =

10.  _csc u cot u  du =

11.  _sec u tan u  du =

12.  _sec u du =

13.  _csc u du =

14.  º du/u

15.   _eudu =

16.  _auu'dx = º audu = ºeu ln a du =

17.  _tan u  du =

18.  _cot u  du =

19.  _sin2u  du =

20.  _cos2u  du =

21.  _tan2u  du =

22.  _cot2u  du =

23. 

 

24. 

 

25. 

 

26.  deg P ³deg Q, use long division first

 

27. 

28.  , use trig substitution

Calculus  DIFFERENTIATION AND INTEGRATION Table ( u = u(x))

1.  Dx(c) = 0

2.  Dx(c f(x)) = c Dx( f(x))

3.  Dx(xn) = n xn-1

4.  Dx(un) = n un-1 u'(x)

5.  Dx(f ± g) = f '(x)  ± g ' (x)

6.  Dx(fg) = f ' (x) g(x) + g ' (x)  f(x)

7.  Dx(f/g)=(f '(x) g(x) - g '(x) f(x)) / (g(x))2

8.  Dx(f(u(x)) = (df/du)(du/dx) = f '(u) u '(x)

9.  Dx(sin u) = u '(x) cos u

10.  Dx(cos u) = - u '(x) sin u

11.  Dx(tan u) = u '(x) sec2 (u)

12.  Dx(csc u) = - u '(x) csc u cot u

13.  Dx(sec u) = u '(x) sec u tan u

14.  Dx(cot u) = - u '(x) csc2 u

15.  Dx(eu) = eu u '(x)

16.  Dx(au) = au u '(x)  ln a

17.  Dx(ln u) = u '(x) / u

18.  Dx(logau) = u '(x) / (u  ln a)

19.  Dx(Arcsin u) = u '(x) / (1 - u2) 1/2

20.  Dx(Arctan u) = u ' (x) / (1 + u2)

21.  Dx(Arcsec u) = u ' (x) / (u (u2 - 1)1/2)

22.  Dx(sinh u) =

23.  Dx(cosh u) =

24.  Dx(tanh u) =

25.  Dx(sech u) =

26.  Dx(csch u) =

27.  Dx(coth u)

1.  º c dx = cx  + C

2.  º c f(x)dx = cºf(x)dx

3.  _xndx =  xn+1 / (n+1)           for n ­ -1

4.  _unu'dx = º un du = un+1 /(n+1)         for n ­ -1

5.  º(f ± g)dx = º f dx ± º g dx

6.  _sin u du = - cos u + C

7.  _cos u  du = sin u + C

8.  _sec2 u  du = tan u + C

9.  _csc2u  du = - cot u + C

10.  _csc u cot u  du = - csc u + C

11.  _sec u tan u  du = sec u + C

12.  _sec u du = ln | sec u + tan u| + C

13.  _csc u du = ln |csc u - cot u| + C

14.  º du/u = ln |u| + C

15.   _eudu = eu + C

16.  _auu'dx = º audu = ºeu ln a du = au / ln a + C

17.  _tan u  du = - ln |cos u| + C or ln | sec u| + C

18.  _cot u  du = ln | sin u| + C

19.  _sin2u  du =  (1/2) (u - (sin2u)/2 ) + C

20.  _cos2u  du = (1/2) (u + (sin 2u)/2) + C

21.  _tan2u  du = tan u - u + C

22.  _cot2u  du = - cot u - u + C

23. 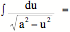  arc sin (u/a) + C

 

24. 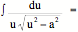  (1/a) arc sec (u/a) + C

 

25. 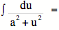  (1/a)arc tan (u/a) + C

 

26. 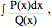 deg P ³deg Q, use long division first

 

27. 

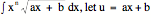
28. 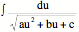 , use trig substitution