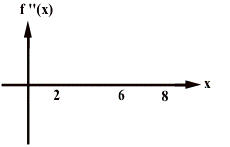Math 125      Final   10 points each    May 4, 2005

Instructor:  K.W.Nicholson

 

1. Use the piecewise continuous function below for parts a & b .

 

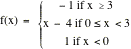  , Find:

 

a.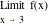  

 

 

 

b. 

 

 

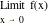
2.    Write down the algebraic definition of the derivative of y = f(x) at (xo, f(xo)).

 

 

 

 

 

 

 

 

 

 

 

 

3.  Find the equation of the line tangent to

 

y = ex cos x at the point (0,1).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.   Find y' = dy/dx

 

x ey - 10 x + 3y = 10

 

 

 

 

 

 

 

 

 

 

 

 

 

Evaluate the integral

 

5. 

 

 

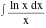
6. 

 

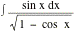
7.  Evaluate the definite Integral

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

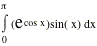
8.  Find x & y intercepts, vertical and horizontal asymptotes, max's, min's, inflection points and sketch

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

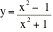
9.  Find the area bounded by y = x2 -x , the x axis,

 x = 0 , and x = 4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

10.   A box with a square base is to have an open top.  The area of the material in the box is to be 100 in2.  What should the dimensions be in order to make the volume as large as possible?

 

 

10  Points Bonus:

 

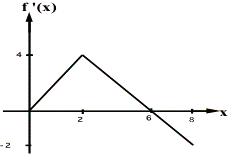
Draw the f(x) vs x  and fÕÕ(x) vs x  (assume the object starts at the origin ) graphs for the given fÕ(x) vs x graph.