1.
Find the equation of the line tangent to (x +
2.
Find dx/dt for y = x2 - 3x when x = 1 and dy/dt = 2
3. Find the rate of change of the distance between
the origin and a point moving on the graph of y = sin x if dx/dt = 2.
4. Related Rate Problem:
¥ 2
points Draw a picture and
Label picture (if appropriate)
¥ 2
points Describe all
variables involved and state clearly what you are trying to find.
¥ 2
points Find equation
relating the variables
¥ 2
points Differentiate
w.r.t. time
¥ 2
points Substitute in
known values to solve for desired quantity
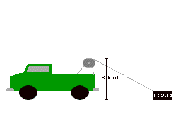
A winch on a motionless truck 6 feet above
the ground is dragging a heavy load as indicated below. If the winch pulls the cable at a
constant rate of 1.5 ft / second, how quickly is the load moving on the ground
when it is 11 feet from the truck?
5.
Find max and min points and tell whether they are relative or absolute.
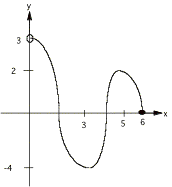
Find all max and min points and tell
whether relative or absolute.
6. f(x) = - x2 + 6x
7.
f(x) = x2(3 - x)
8.
f(x) = x2 - 4x
on [-1 , 3]
9.
f(x) = sin2 x +
cos x on [0, ¹]
10.
Draw a function that has an
absolute max at x = 2
absolute minimum at x = -1
relative max at x = 0
Bonus Problems, 10 Pts!
A triangle is shrinking. Find the rate of change of area when
the area is 30 square inches and the height is decreasing at a rate of 3 inches
/ second at the instant that the base is 6 inches.