For the function in the graph:
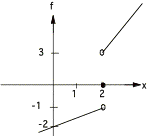
1.
At which value of x does the limit not exist ?
2.
Find ![]() .
.
Consider the piecewise continuous function
![]() , Find:
, Find:
3. ![]()
4.
![]()
5.
![]()
If ![]() and
and ![]() ,
,
use the Rules for Limits to evaluate:
6.![]()
7.
![]()
8.
![]()
Evaluate the limits.
9. ![]()
10. ![]()
11.
![]()
Find the equation(s) of the Vertical
Asymptote(s) for:
12.
![]()
13. ![]()
14.
![]()
15. If D represents the number of deer amd W represents the number of wolves
in the forest as a function of time,
a.
What sign would you expect dD/dW to have?
b.
What sign would you expect dW / dD to have?
16.
Give the algebraic definition of the derivative of y = f(x) at the point
(a, f(a)). You must use a complete sentences to get any credit at all.
17. Find the slope of the line tangent to
f(x) = 4x2 - 3x - 1 at x = 1.
18.
Draw the f(x) vs x and fÕÕ(x) vs x (assume the object starts at the origin
) graphs for the given fÕ(x) vs x graph.
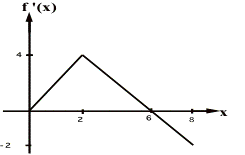
Differentiate the function: (means find f ' (x) ).
19.
f(x) = x + 1
20.
f(x) = 4 x2 - 3 x - 6
21.
f(x) = sin x
22.
![]()
23.
f(x) = x2 sin (x)
24.
f(x) = cos (5x2)
25.
![]()