Differentiate
1.
2. 
3.
y = sec 4x cos x2
4. y = ¹ tan20 4x
5. 
6. Find the equation of the line
tangent to
f(x) = sin (¹x) at x = 1/3
Find all max and min and sketch the
function.
7.
on the interval [-1,2]
Sketch Graph without calculus:
8. y = (x - 2)2 (x + 3)3 (x - 1)2
9.
Find max's, min's, inflection points
and sketch accurate graph of the functions, tell whether each max or min is
relative or absolute.
10. y = x3 - 3x2 + 3
Write the equation for:
11.
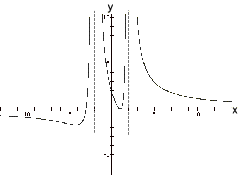
12.
The height of a right triangle remains fixed at 6 m while the base
expands at a constant rate of 3
m/s. Find the rate of change of the
area of the triangle at the instant the base is 8 m.
10 points Bonus!
Find max's, min's, inflection points
and sketch accurate graph of the functions, tell whether each max or min is
relative or absolute.
