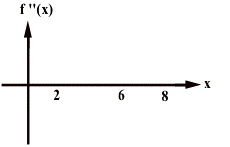Math 125 Final Part II 10 points each May 1, 2006

Instructor: K.W.Nicholson

1. Use the function in the graph below for a & b

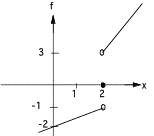
a. At which value(s) of x does the limit not exist ?

b. Find .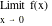

2. Write down the graphical definition of the derivative of y = f(x) at (x_o, f(x_o)).

3. Find the equation of the line tangent to

y = e^x sin x at the point (0,0).

4. Find y' = dy/dx

x sin y - 10 x + 3y = 10

Evaluate the integral

5.

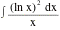
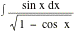
6.	7. Evaluate the definite Integral

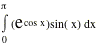
8. Find x & y intercepts, vertical and horizontal asymptotes, max's, min's, inflection points and sketch

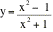
9. Find the area bounded by y = x² -x , the x axis,

x = 0 , and x = 4

10. A farmer wishes to build a rectangular shaped pen for her chickens with a fixed area of 30,000 sq meters that has two compartments as indicated in the figure below. Since one side borders a river and chickens are afraid of water, she doesn't need to fence the side next to the river. Determine the dimensions of the pen that will use the least amount of fencing.

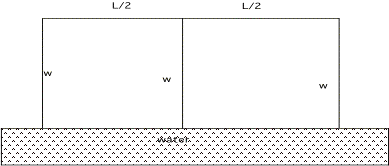
10 Points Bonus:

Draw the f(x) vs x and f’’(x) vs x (assume the object starts at the origin ) graphs for the given f’(x) vs x graph.
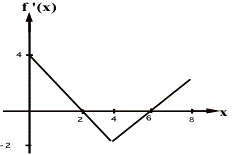