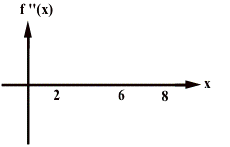Math 125 Final 20 points each May 1, 2007

Instructor: K.W.Nicholson

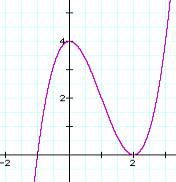
1. Given f(x) below:

a. Find

b. Find .

Use the function in the graph below for c & d

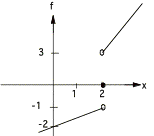
c. At which value(s) of x does the limit not exist ?

d. Find .

2. a. Write down the graphical definition of the derivative of y = f(x) at (x_o, f(x_o)).

2b. Find the equation of the line tangent to

y = 4x² - 5x +2 at x = 2.

3. Draw a function with:

a. positive derivatives

b. positive derivatives then zero, then negative derivatives

c. increasing derivatives

d. decreasing derivatives

4. (2 points each)

Differentiate

a. y = sin π

b. y = log₄ x²

c.

d.

e.

Integrate:

f. ∫ 4x⁶ dx

g. ∫ 5^x dx

h. ∫ (1 + tan²x ) dx

i. ∫ e^4x dx

j.

5. Find y ' = dy/dx

x sin y - 10 x + 3y = 10

6. Find all max & mins for

f(x) = x³ - 6x² for -2 ≤ x ≤ 8

7. a. Find x & y intercepts, HA & VA and sketch

7b. Find the equation for the function whose graph is:

8. Find x & y intercepts, vertical and horizontal asymptotes, max's, min's, inflection points and sketch

9. A farmer wishes to build a rectangular shaped pen for her chickens with a fixed area of 30,000 sq meters that has two compartments as indicated in the figure below. Since one side borders a river and chickens are afraid of water, she doesn't need to fence the side next to the river. Determine the dimensions of the pen that will use the least amount of fencing.

10. A 20 ft ladder leaning against a wall is sliding down the wall so that the the bottom is moving away from the wall 5 ft/s . How fast is the top moving down the wall at the instant the bottom is 16 ft from the wall ?

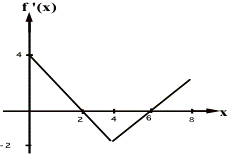
10 Points Bonus:

Draw the f(x) vs x and f’’(x) vs x (assume the object starts at the origin ) graphs for the given f’(x) vs x graph.